The equation 24x²+25x-47ax-2=8x-3-53ax-2 is true for all values of x≠2 where a is a constant. What is the value of a?

For those who have already taken the Scholastic Aptitude Test (SAT) or the American College Testing (ACT), you may have encountered a question similar to above. Many of you may have thought, “What kind of a question is this? What kind of person even knows how to solve this?” When taking any standardized test, you are given a certain amount of questions—typically a large amount—and you are given a certain amount of time—typically a small amount. In the time crunch that you are given for the math section of the SAT, you are expected to answer each of the 44 questions in roughly one minute and 30 seconds. This raises the question of who can successfully perform well on this test; simply, it is those who can financially afford to do so.

During the mid-19th century, millions of immigrants from Europe came to the United States. Coincidentally, standardized testing in America started during the mid-19th century. According to the National Education Association, leading social scientists at this time—many of whom were eugenic White Anglo-Saxon Protestants—did not want to include non-white people in the American educational system.

A century after standardized testing was introduced to the nation, college officials still favored the SAT as it was believed during the 1920s that intelligence and ethnic origin were correlated to each other. Thus, the results were observed through this belief, which began limiting ethnicities in the admission process.

Throughout the 1950s and 1960s, the top universities in the U.S.—Harvard, Yale, and Princeton—were on the hunt for smart students, regardless of their ethnicity (2005, Karabel). This hunt did not close the racial gap in college enrollment since, according to FairTest, students from communities of color were failing high school graduation exams.

Standardized testing has not been entirely inclusive to students of color. Thanks to modern technology, people with less access to prepare for the SAT and ACT are now more able to do so with free online materials. However, these tests have been increasingly more expensive to simply sign up for (as of this year, an ACT can cost up to $88). Therefore, those who can afford to take multiple tests have a much greater chance of obtaining a higher score compared to someone who cannot.

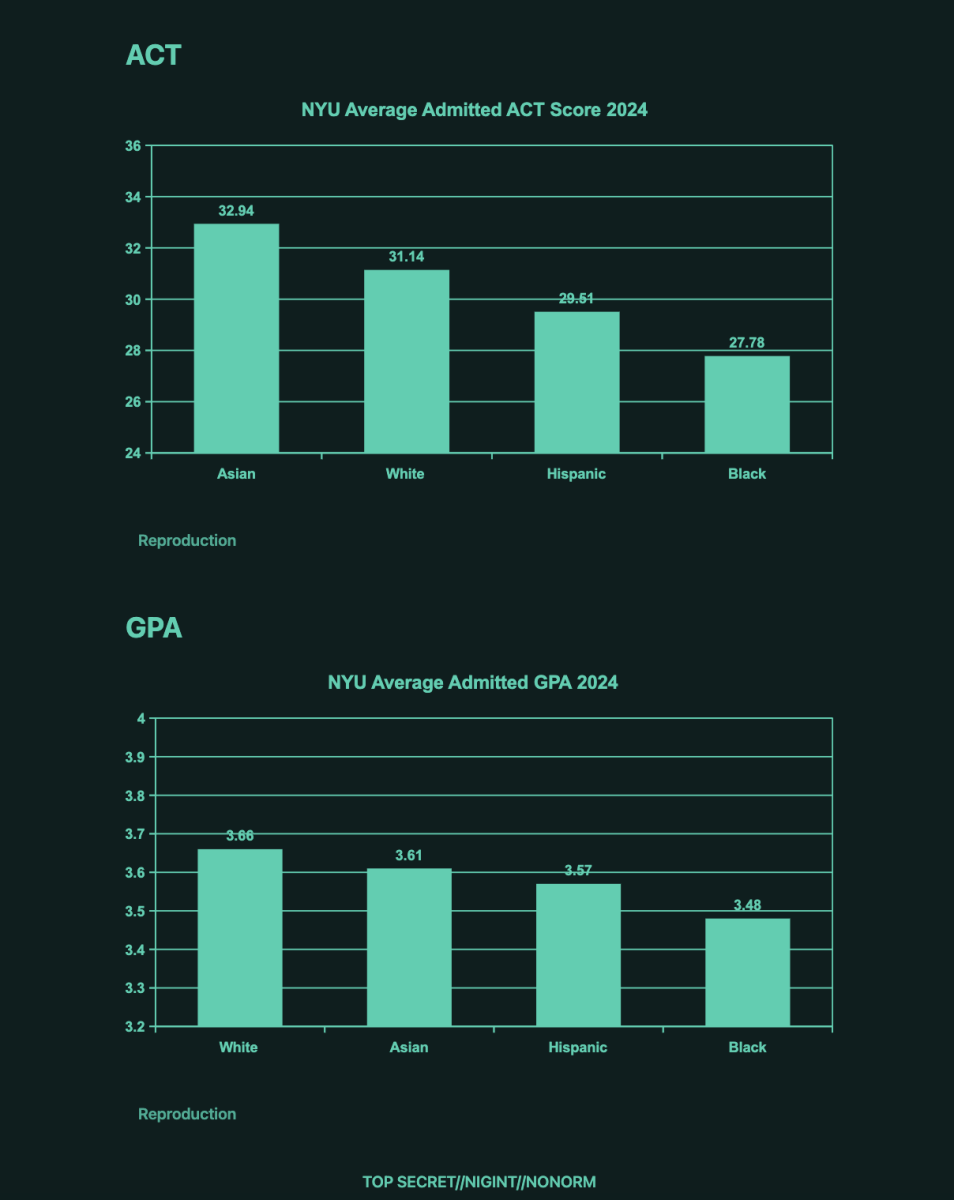
According to a study from the University of Southern California, students who are from a household earning 200,000 a year or more average a combined score of 1626, while students who are from a household earning under 20,000 average a combined score of about 1326. Additionally, the difference between high-income to low-income students’ SAT scores was almost double for black students than white students. 

Despite years of multiple top-tier schools being “test-optional” for admission, there is a new push to bring back; many more schools require standardized testing scores to be submitted again. The question remains, “What’s the point?” Not only does standardized testing not accurately measure intelligence, but it is also inaccessible to lower-income students. While schools like Brown and Yale have switched to that you may submit AP or I.B., or dual credit scores in place of SAT or ACT, that still does not solve the problem of accessibility as those are typically offered more frequently at a higher level, private schools.

Our opinion is, scores do not add a lot to a college application. While there are students who can have a very high score that could help differentiate them, they serve no real purpose for those who did not receive the same- for whatever reason that may be. Even though this can help certain students stand out, they can still submit those without mandating others to do the same. The college process is a long and stressful process where each student wants to show the best of their last four years. their entire application should not be scrapped because they had a bad Saturday where they could not answer “the equation 24x²+25x-47ax-2=8x-3-53ax-2 is true for all values of x≠2 where a is a constant. What is the value of a?” correctly. It is unfair to praise some individuals for the opportunities they may have been given while dismissing others who were not given the same.